Какво е RSA криптография? Пълно ръководство за този алгоритъм за шифроване

Криптографията се използва в цивилизациите в различни формати в продължение на хиляди години. От древните египтяни до съвременния Интернет, използването на криптография за криптиране и дешифриране на съобщения е жизненоважен инструмент за комуникация.

RSA криптографията (по-точно RSA алгоритъмът) е най-повсеместният асиметричен алгоритъм за криптиране в света. Стана възможно чрез редица криптографски и математически пробиви, всеки, който използва Интернет, използва RSA криптография под някаква или друга форма.

Повечето криптовалути използват подобен тип асиметрично криптиране като RSA, известен като криптография с елиптична крива. Макар и различни, и двамата се основават на сходни концепции и разбирането на RSA е важно за по-нататъшното разбиране на криптографията, използвана в мрежите за криптовалута.

Криптографски фон и симетрична срещу асиметрична криптография

До 70-те години криптографията се основава предимно на използването на симетрични ключове. В симетричните ключови алгоритми двама потребители, които искат да комуникират съобщение помежду си, използват едни и същи криптографски ключове както за криптиране на обикновения текст, така и за декриптиране на шифротекста. Ключовете представляват споделена тайна между двете страни и могат да се използват като частна форма на комуникация. Въпреки това има някои присъщи проблеми с този дизайн, което води до някои сериозни недостатъци при използването му.

Например и двете страни трябва да знаят тайния ключ, за да кодират и дешифрират съобщението. Извън личното съвещание за обмен на тази информация, има значително количество комуникационни разходи, необходими за постигането на това в частен план чрез средства, които не са сигурни. Трети страни, които гледат тези канали, могат да получат секретния ключ и по този начин методът на криптиране се компрометира. Освен това концепцията за симетрично криптиране на ключове не е мащабируема. Ако искате да изпращате криптирани съобщения до множество хора, ще трябва да запомните таен ключ за всяка от тези линии за комуникация. Очевидно това бързо става неудобно и очевидно не е най-добрият модел за използване от криптовалутни мрежи, където се обменя стойност.

Решението за това дойде под формата на това, което е известно като асиметрично криптиране или по-популярно наричано криптография с публичен ключ. Асиметричното криптиране използва два ключа, публичен ключ и частен ключ. В най-основната форма на този модел потребителят може да публикува публичен ключ, с който всеки друг може да използва, за да изпрати на това лице криптирано съобщение и само лицето, което е публикувало публичния ключ и има съответния частен ключ, може да дешифрира и прегледа това съобщение. Използването на единия ключ отменя използването на другия и ключовете не трябва да се обменят между страните, които желаят да общуват.

Моделът на асиметрично криптиране стана възможен чрез 2 брилянтни принципа, дошли в резултат на пробив на британския математик Джеймс Елис през 1970 г. Елис описа идея, при която криптирането и декриптирането са обратни операции помежду си въз основа на 2 различни ключа.

Джеймс Елис, изображение от Телеграфът.

Концепцията обикновено е представена от катинар и ключ, като катинарът представлява публичен ключ, а ключът представлява частен ключ. За да се използва на практика тази теория, се развиха два принципа.

Функцията на капака

Функцията на вратичката е много важна концепция в криптографията, при която е тривиално да се премине от едно състояние в друго състояние, но да се изчисли в обратна посока чрез връщане в първоначалното състояние става невъзможно без специална информация, известна като „капака“.

Нарича се най-известната днес функция на капака, която е в основата на RSA криптографията Главно разграничаване. По същество основната факторизация (известна също като целочислена факторизация) е концепцията в теорията на числата, че съставните цели числа могат да бъдат разложени на по-малки цели числа. Всички съставни числа (непрости числа), които са разбити до най-основните са съставени от прости числа. Този процес е известен като основно факторизиране и има сериозни последици, когато се прилага към криптографията.

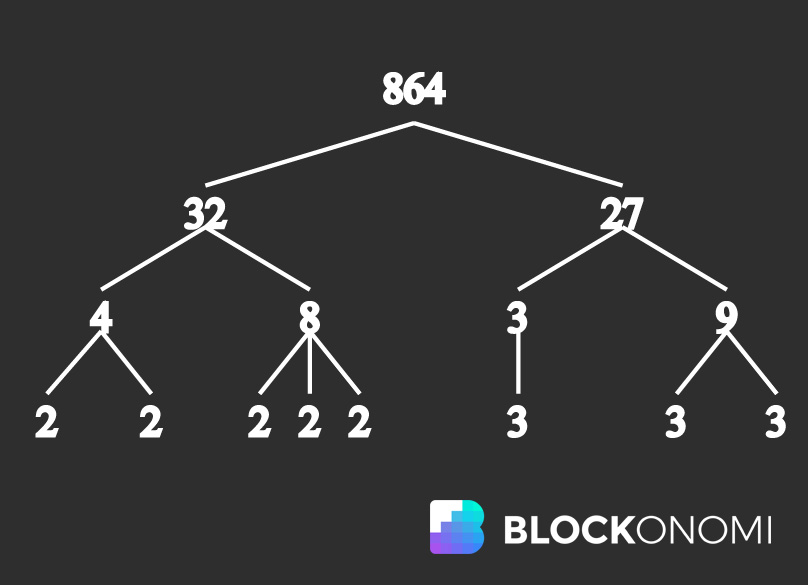
Главна факторизация, Изображение, използвано от Уикипедия

По същество, разлагането на първостепенни фактори на изключително големи прости числа става невъзможно да се изчисли поради огромното количество проби и грешки, необходими за успешното разлагане на числото на най-основните му компоненти. Понастоящем не съществува ефективен алгоритъм за факторизиране, който да изпълнява това.

RSA и как той използва първостепенно факторизиране е описано в следващ раздел, но първо трябва да разберем Diffie-Hellman Key Exchange.

Размяната на ключове на Diffie-Hellman

Обменът на ключове Diffie-Hellman е един от първите криптографски протоколи с публичен ключ и по същество позволява сигурен обмен на криптографски ключове на публичен носител. За по-голяма простота, опитът да се концептуализира Diffie-Hellman Key Exchange и следващият раздел за това как работи алгоритъмът RSA е много по-тривиален с абстрактни понятия в сравнение с чистата математика, така че ще прилагаме математиката само когато е необходимо.

Най-често срещаният пример, използван за концептуализиране на размяната на ключове Diffie-Hellman, е известен като Secret Color Exchange.

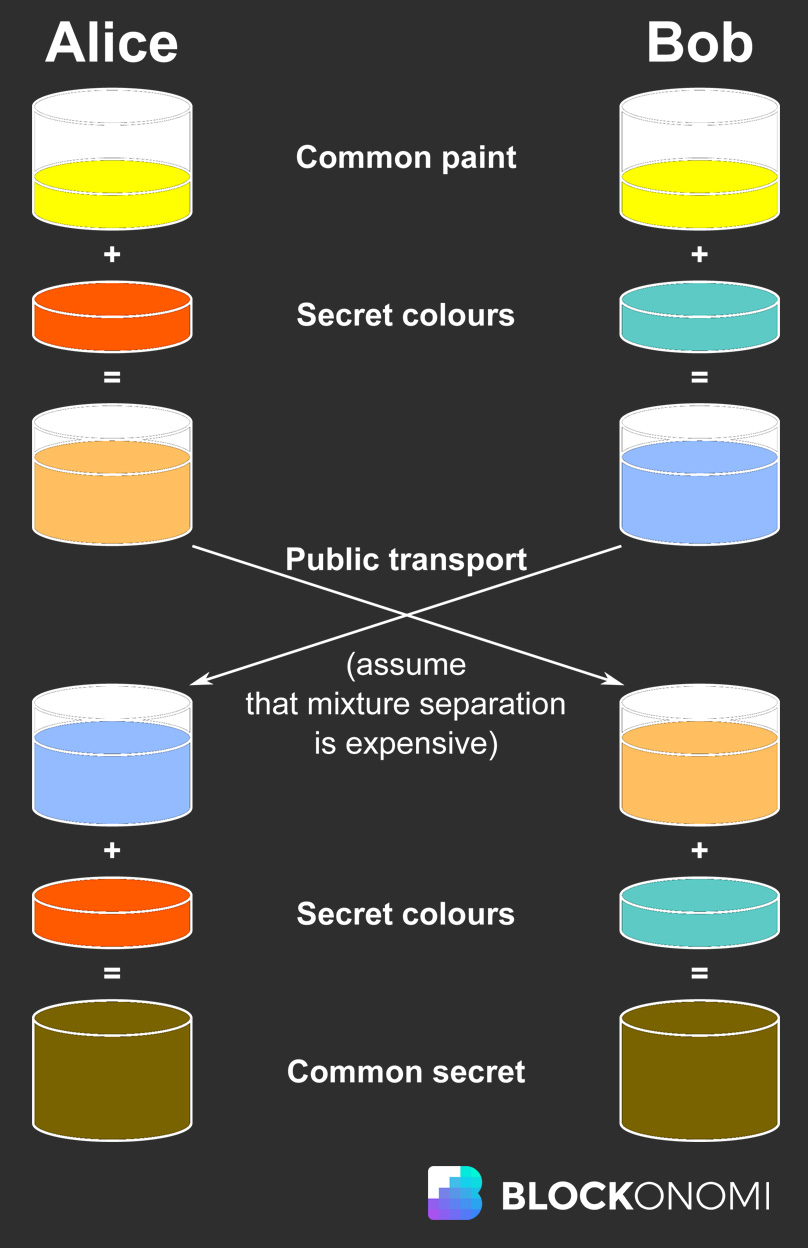
Обмен на ключове Diffie-Helman, изображение, използвано от Уикипедия

Горната снимка представлява линия за комуникация между Алис и Боб по публичен канал, където Ив може да слуша всичко, което публично се комуникира между Алис и Боб. И така, как могат Алис и Боб да комуникират лично съобщение, използвайки асиметрично криптиране, без изрично да обменят тази информация на публичния носител?

Те обменят тайна информация помежду си, без всъщност да я споделят. Процесът работи по следния начин:

Етап 1

Алис и Боб се съгласяват, че жълтото е често използваната боя. Тази информация се излъчва по обществения канал, така че и Ева да знае това.
Жълтото представлява публичния ключ.
Алис решава тайно, че ще използва и синьо заедно с жълто, а Боб тайно решава, че ще използва червено с жълто.
Синьото, използвано от Алиса, и червеното, използвано от Боб, представляват техните тайни ключове.

Стъпка 2

След това и Алис, и Боб се смесват в своите тайни цветове с жълто, за да създадат композитен цвят.
Миксът на Alice’s създава Green, а Mix на Bob – Orange.
Сега и Алис, и Боб си изпращат взаимно своите композитни цветове.
Ева също получава тези цветове, но се сблъсква с проблем, тези композитни цветове представляват функция капан.
Лесно е да се комбинират два цвята, за да се получи трети цвят, но е невъзможно да се обърне това. Много е трудно да се определи кои цветове са използвани за създаване на третия цвят само от третия цвят и оригиналния жълт.

Стъпка 3

След това Алис и Боб смесват своите тайни цветове с получените композитни цветове, което води до следното.

Алис смесва синьото с композитния портокал от Боб.
Боб смесва червеното с композитното зелено от Алиса.
И двете смеси водят до кафяво.

Това е тайната на размяната на ключове Diffie-Hellman. Въпреки че и Алис, и Боб се оказаха с Браун, те всъщност никога не си размениха този цвят и Ева остава без необходимата информация за тайните цветове, за да може да изчисли тайното съобщение (Браун).

Примерът по-горе е много проста визуализация на това как работи обменът. С приложената математика може да се постигне гарантирана сигурност и целостта на съобщенията чрез RSA криптография, като се използва главно факторизиране като капак.

Как работи алгоритъмът RSA?

Алгоритъмът RSA работи, като използва основния капак за факторизация и обмена на ключове Diffie-Hellman, за да постигне асиметрично криптиране. По принцип RSA криптографията разчита на трудността на първостепенното разлагане като метод за сигурност. Използвайки много опростен пример с описана ограничена математика, алгоритъмът RSA съдържа 4 стъпки.

Генериране на ключове – По време на тази стъпка потребителят може да използва генератор на случайни числа или просто да избере 2 много големи прости числа (наречени p и q). Тези номера трябва да се пазят в тайна. Изчислете n = pq, където „n“ е модулът както за публичните, така и за частните ключове и дължината му е известна като дължина на ключа. Направете „n“ публично. За ключови размери, равни или по-големи от 1024 бита, няма ефективен метод за ефективно решаване на този алгоритъм (факторизиране на много големия брой „n“). Дори най-големият суперкомпютър в света ще отнеме хиляди години, за да го реши. Това е известно като RSA проблем и ако бъде решен, ще компрометира всички базирани на RSA криптосистеми.
Разпределение на ключове – Боб иска да изпрати на Алис секретна информация, така че да се извършват следните стъпки.

Боб трябва да знае публичния ключ на Алис, за да шифрова съобщението.
Алиса трябва да знае личния си ключ, за да дешифрира съобщението.
За да може Боб да изпрати криптираното си съобщение, Алис изпраща публичния си ключ на Боб.
Алис никога не разпространява личния си ключ.

Шифроване – След като Боб получи публичния ключ на Алис, той може да изпрати съобщение (М) до Алис. Първо, той превръща (M) (в този момент съобщение с открит текст) в цяло число (m) чрез използване на договорена схема за подплата. След това той изчислява шифъртекста, използвайки публичния ключ на Алиса и предава (в) на Алис.

Дешифриране – Алиса може да възстанови съобщението (m) от шифъртекста (c), като използва личния си ключ. След това тя може да възстанови оригиналното съобщение (M), като обърне схемата за подплънки от (m).

Може да се намери по-задълбочено обяснение на математическите операции, използвани в RSA тук, но е извън обхвата на тази статия.

В допълнение, RSA криптирането позволява цифрово подписване на съобщения, което е от първостепенно значение за криптовалутите и е ключов компонент на модела на транзакции UTXO на Биткойн. Алис може да подпише цифрово съобщение до Боб, за да потвърди, че го е изпратила (като потвърди, че е използван нейният личен ключ), като създаде хеш стойност на съобщението и го прикачи към съобщението. Тази стойност може да бъде проверена от Боб, който използва същия алгоритъм на хеширане заедно с публичния ключ на Алис и сравнява получената хеш стойност с действителната хеш стойност на съобщението.

Заключение

RSA криптирането е най-широко използваният метод на асиметрично криптиране в света поради способността му да осигурява високо ниво на криптиране, като все още не съществува известен алгоритъм, за да може да го реши. Въз основа на някои брилянтни пробиви в криптографията и математиката, включително обмена на ключове Diffie-Hellman и функцията на капака, RSA криптирането стана първостепенно за осигуряване на комуникация по целия свят.