Elliptic Curve Cryptography คืออะไร? เทคโนโลยีเบื้องหลังลายเซ็นดิจิทัลในสกุลเงินดิจิทัล

การเข้ารหัสเป็นรากฐานของรูปแบบลายเซ็นดิจิทัลของสกุลเงินดิจิทัลและเป็นพื้นฐานสำหรับการตรวจสอบธุรกรรมที่ปลอดภัยระหว่างสองฝ่ายผ่านเครือข่ายแบบกระจายอำนาจ ปัจจุบันมีวิธีการเข้ารหัสจำนวนมากที่ใช้โดยสกุลเงินดิจิทัลต่างๆโดยมุ่งเน้นไปที่การจัดหารูปแบบการทำธุรกรรมที่มีประสิทธิภาพและปลอดภัย.
Elliptic Curve Cryptography (ECC) เป็นหนึ่งในวิธีการที่ใช้กันอย่างแพร่หลายสำหรับรูปแบบลายเซ็นดิจิทัลในสกุลเงินดิจิทัลและรูปแบบเฉพาะคือ Elliptic Curve Digital Signature Algorithm (ECDSA) ถูกนำไปใช้ทั้งใน Bitcoin และ Ethereum สำหรับการลงนามธุรกรรม.

ความเป็นมาของ ECC และ ECDSA
Elliptic Curve Cryptography ได้รับการแนะนำโดยนักคณิตศาสตร์ Neal Koblitz และ Victor S Miller โดยอิสระในปี 1985 ในขณะที่ความก้าวหน้าในการเข้ารหัส ECC ไม่ได้ใช้กันอย่างแพร่หลายจนถึงต้นปี 2000 ในช่วงที่อินเทอร์เน็ตเกิดขึ้นซึ่งรัฐบาลและผู้ให้บริการอินเทอร์เน็ตเริ่มใช้มัน เป็นวิธีการเข้ารหัส.
เมื่อเทียบกับการเข้ารหัส RSA ECC มีข้อได้เปรียบที่สำคัญ ขนาดคีย์ที่ใช้สำหรับ ECC นั้นเล็กกว่าที่จำเป็นสำหรับการเข้ารหัส RSA มากในขณะที่ยังคงให้ความปลอดภัยในระดับเดียวกัน แม้ว่าการเข้ารหัส RSA จะใช้กันอย่างแพร่หลายบนอินเทอร์เน็ตในปัจจุบัน แต่ ECC เป็นรูปแบบ RSA ที่มีประสิทธิภาพมากขึ้นซึ่งเป็นหนึ่งในเหตุผลหลักที่ใช้ในสกุลเงินดิจิทัล.

อ่าน: RSA Cryptography คืออะไร? คู่มือฉบับสมบูรณ์สำหรับอัลกอริทึมการเข้ารหัสนี้
สถาบันมาตรฐานและเทคโนโลยีแห่งชาติของสหรัฐอเมริกา (NIST) รับรอง ECC ในฐานะ“ห้องชุด B” อัลกอริทึมที่แนะนำและ NSA สนับสนุนอย่างเป็นทางการในการจำแนกข้อมูลลับสุดยอดด้วยคีย์ 384 บิต ตัวอย่างประสิทธิภาพของ ECC เมื่อเทียบกับ RSA คีย์ 384 บิตเดียวกันที่ใช้ในการเข้ารหัสข้อมูลลับจะต้องใช้คีย์ 7680 บิตโดยใช้การเข้ารหัส RSA ประสิทธิภาพที่ ECC มอบให้จึงมีประโยชน์อย่างมากต่อเครือข่ายบล็อกเชนเนื่องจากช่วยลดขนาดของธุรกรรม.
มันทำงานอย่างไร
Elliptic Curve Cryptography เป็นวิธีการ คีย์สาธารณะ การเข้ารหัสตามฟังก์ชันพีชคณิตและโครงสร้างของเส้นโค้งบนกราฟ จำกัด ใช้ฟังก์ชันประตูระบายที่ระบุไว้ในความเป็นไปไม่ได้ในการกำหนดลอการิทึมแบบไม่ต่อเนื่องขององค์ประกอบเส้นโค้งวงรีแบบสุ่มที่มีจุดฐานที่เป็นที่รู้จักของสาธารณชน.
ฟังก์ชัน Trapdoor ใช้ในการเข้ารหัสคีย์สาธารณะเพื่อให้เป็นเช่นนั้นโดยเริ่มจาก A -> B เป็นเรื่องเล็กน้อย แต่ไปจาก B -> A เป็นไปไม่ได้โดยใช้ประโยชน์จากปัญหาทางคณิตศาสตร์ที่เฉพาะเจาะจง ตัวอย่างเช่นการเข้ารหัส RSA ขึ้นอยู่กับแนวคิดของ ตัวประกอบที่สำคัญ, และ ECC อาศัยแนวคิดของ การคูณจุด, โดยที่ตัวคูณแสดงถึงคีย์ส่วนตัวและไม่สามารถคำนวณได้จากจุดเริ่มต้นที่กำหนด.
เส้นโค้งรูปไข่ต้องประกอบด้วยจุดที่ตรงตามสมการ:
y ^ 2 = ขวาน ^ 3 + b
(x, y) บนเส้นโค้งแสดงถึงจุดในขณะที่ทั้ง a และ b เป็นค่าคงที่ ในทางทฤษฎีมีเส้นโค้งที่ไม่สิ้นสุดที่สามารถสร้างขึ้นได้ แต่ใช้เฉพาะกับสกุลเงินดิจิทัล (ในกรณีของ Bitcoin และ Ethereum) เส้นโค้งวงรีที่เรียกว่า secp256k1 ถูกนำมาใช้. มันแสดงอยู่ในภาพด้านล่าง.
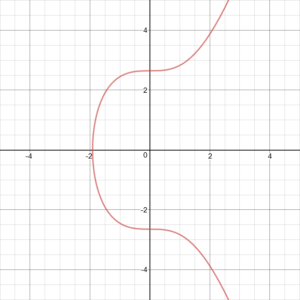
อย่างที่คุณเห็นเส้นโค้งวงรีนั้นสมมาตรเกี่ยวกับแกน x ด้วยเหตุนี้หากคุณลากเส้นตรงโดยเริ่มจากจุดสุ่มบนเส้นโค้งเส้นนั้นจะตัดส่วนโค้งไม่เกิน 3 จุด คุณลากเส้นผ่านสองจุดแรกและกำหนดจุดที่เส้นตัดกับจุดที่สาม จากนั้นคุณจะสะท้อนจุดที่สามนั้นบนแกน x (มันสมมาตร) และจุดนั้นเป็นผลมาจากการบวกสองจุดแรกเข้าด้วยกัน นี่แสดงให้เห็นในภาพด้านล่าง.
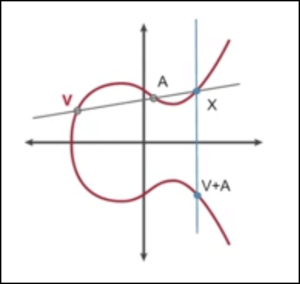
ในกราฟด้านบน V และ A แสดงถึงจุดเริ่มต้น X หมายถึงจุดที่สามและจุดสุดท้าย (เรียกว่า Z) แทนการเพิ่ม V และ A เข้าด้วยกัน เมื่อใช้ในโครงร่างลายเซ็นดิจิทัลโดยทั่วไปจุดฐานของเส้นจะถูกกำหนดไว้ล่วงหน้า.
สำหรับ ECC ในการสร้างฟังก์ชันประตูลับการเข้ารหัสเส้นโค้งวงรีจะใช้การคูณจุดโดยที่จุดฐานที่ทราบจะถูกเพิ่มซ้ำ ๆ ให้กับตัวมันเอง ในกรณีนี้ให้ใช้จุดฐาน P โดยที่เป้าหมายคือการหา 2P ตามที่ระบุไว้ด้านล่าง.
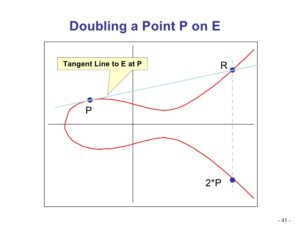
ด้านบนแทนเจนต์วิ่งจากจุด P ถึงจุด R ซึ่งเป็นจุดตัดกัน การสะท้อนของจุดนั้นคือ 2P สมมติว่าเราต้องการดำเนินการต่อไปและค้นหา 3P, 4P และอื่น ๆ ต่อไปเราจะเข้าร่วม P และ 2P และต่อมาสะท้อนจุดนี้เหนือจุดตัดและทำสิ่งนี้ต่อไปสำหรับ 4P ภาพประกอบด้านล่าง:
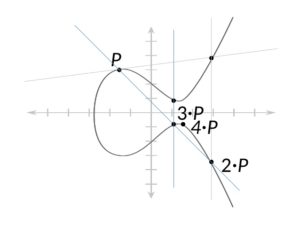
นี่คือคุณสมบัติการคูณของกราฟเนื่องจากเรากำลังหาจุดที่เป็นการคูณของจำนวนเต็มด้วยจุดนั้นเอง ผลลัพธ์ที่ได้คือสิ่งที่ให้ฟังก์ชันประตูประตูหรือที่เรียกว่า ปัญหาลอการิทึมไม่ต่อเนื่อง.
ถ้าเราแทนค่าตัวแปร x เป็นจำนวนเต็ม 384 บิตและคูณด้วยจุดฐาน P ผลลัพธ์คือจุดบนเส้นโค้งเรียกว่า Z ใช้กับสกุลเงินดิจิทัล Z เป็นสาธารณะ แต่ตัวแปรเดิม x เป็นความลับ (ส่วนตัว สำคัญ). ในการกำหนด x จาก Z และ P คุณจะต้องกำหนดจำนวนครั้งที่เพิ่ม P ให้ตัวเองเพื่อให้ได้จุด Z บนเส้นโค้ง ปัญหานี้เป็นรูปแบบของ เลขคณิตแบบแยกส่วน นั่นเป็นไปไม่ได้ทางคณิตศาสตร์และเหตุใด ECC จึงปลอดภัย.
ใช้ใน Cryptocurrencies
เมื่อวิเคราะห์ความจำเป็นในการใช้รูปแบบลายเซ็นดิจิทัลในสกุลเงินดิจิทัลมีข้อกำหนดหลัก 4 ประการของรูปแบบที่กำหนดซึ่งต้องปฏิบัติตามเพื่อให้รูปแบบลายเซ็นเป็นของจริงและพิสูจน์ได้ ซึ่งรวมถึง:
- ควรพิสูจน์ได้ว่าเป็นผู้ลงนามในการทำธุรกรรมเป็นผู้ลงนาม.
- ลายเซ็นไม่ควรปลอมแปลง.
- ลายเซ็นต้องไม่น่าเชื่อถือหมายความว่าลายเซ็นถือเป็นที่สิ้นสุดและไม่สามารถเชื่อมโยงกับข้อมูลประจำตัวอื่นได้.
- มันควรจะเป็นไปไม่ได้ที่จะคำนวณคีย์ส่วนตัวจากคีย์สาธารณะที่เกี่ยวข้อง.
Elliptic Curve Cryptography เป็นไปตามเงื่อนไขทั้ง 4 ข้อและยังมีประสิทธิภาพเป็นพิเศษในการทำเช่นนั้น การใช้ ECC พิกัด (x, y) ของจุดบนกราฟจะเป็นคีย์สาธารณะของคุณและจำนวนเต็มสุ่ม 384 บิต x จะเป็นคีย์ส่วนตัวของคุณ.
นอกจากนี้ยังเป็นไปได้ที่จะพิสูจน์ให้ใครบางคนเห็นว่าคุณรู้ค่าของ x โดยไม่ต้องเปิดเผยว่า x คืออะไร คุณสมบัตินี้ยังช่วยตอบสนองเงื่อนไขที่จำเป็นสำหรับการใช้งานอย่างยั่งยืนในรูปแบบธุรกรรมลายเซ็นดิจิทัล.
ความกังวลเกี่ยวกับควอนตัม
การใช้ ECC ในรูปแบบลายเซ็นดิจิทัลสำหรับสกุลเงินดิจิทัลมีความปลอดภัยเป็นพิเศษ อย่างไรก็ตามเมื่อไม่นานมานี้มีข้อกังวลเกี่ยวกับศักยภาพในอนาคตของคอมพิวเตอร์ควอนตัมและพลังมหาศาลที่มีความสามารถในการทำลาย ECC แม้ว่าความเป็นไปได้จะถือว่าห่างออกไปหลายปี, อัลกอริทึมของชอร์ ในทางทฤษฎีจะสามารถคำนวณลอการิทึมแบบไม่ต่อเนื่องบนคอมพิวเตอร์ควอนตัมสมมุติที่มีกำลังเพียงพอ.
สกุลเงินดิจิทัลต่างๆได้ใช้แนวทางการคิดล่วงหน้าต่อภัยคุกคามที่อาจเกิดขึ้นจากคอมพิวเตอร์ควอนตัมโดยใช้อัลกอริธึมที่ต้านทานควอนตัมเป็นรากฐานของโครงร่างลายเซ็นดิจิทัล แม้แต่ NSA ในปี 2015 ก็ประกาศการเปลี่ยนแปลงในอนาคตที่วางแผนไว้ออกจาก ECC และไปใช้ชุดรหัสที่แตกต่างกันสำหรับความต้องการในการเข้ารหัสเนื่องจากความสามารถในการประมวลผลควอนตัมที่หลีกเลี่ยงไม่ได้.

อ่าน: คอมพิวเตอร์ควอนตัม: ภัยคุกคามใดที่ก่อให้เกิด Bitcoin?
ความกังวลเหล่านี้ส่วนใหญ่เป็นการคาดเดา ณ จุดนี้เนื่องจากพลังการคำนวณควอนตัมที่จำเป็นสำหรับอัลกอริทึมของ Shor ในการคำนวณลอการิทึมแบบไม่ต่อเนื่องนั้นสูงกว่าคอมพิวเตอร์ควอนตัมขั้นต้นที่มีประสิทธิภาพมากที่สุดในปัจจุบัน.
สรุป
เมื่อมองไปข้างหน้า cryptocurrencies รุ่นต่อ ๆ ไปอาจเปลี่ยนไปใช้วิธีการเข้ารหัสขั้นสูงเพื่อรักษาความปลอดภัยในการทำธุรกรรมของพวกเขาและ Bitcoin และ Ethereum อาจจำเป็นต้องทำการเปลี่ยนแปลงเดียวกัน.
สำหรับตอนนี้ ECC และรูปแบบลายเซ็นดิจิทัลอื่น ๆ ที่ใช้ฟังก์ชันประตูลับยังคงเป็นวิธีการเข้ารหัสที่ปลอดภัยที่สุดในโลกและควรจะยังคงอยู่ต่อไปในบางครั้ง.



