RSA Cryptography คืออะไร? คู่มือฉบับสมบูรณ์สำหรับอัลกอริทึมการเข้ารหัสนี้

การเข้ารหัสถูกใช้ในอารยธรรมในรูปแบบที่แตกต่างกันเป็นเวลาหลายพันปี ตั้งแต่ชาวอียิปต์โบราณไปจนถึงอินเทอร์เน็ตสมัยใหม่การใช้การเข้ารหัสเพื่อเข้ารหัสและถอดรหัสข้อความเป็นเครื่องมือสำคัญในการสื่อสาร.
การเข้ารหัส RSA (อัลกอริทึม RSA ที่แน่นอน) เป็นอัลกอริธึมการเข้ารหัสแบบอสมมาตรที่แพร่หลายมากที่สุดในโลก เกิดขึ้นได้จากการเข้ารหัสและการพัฒนาทางคณิตศาสตร์จำนวนมากใครก็ตามที่ใช้อินเทอร์เน็ตจะใช้การเข้ารหัส RSA ในรูปแบบใดรูปแบบหนึ่ง.

สกุลเงินดิจิทัลส่วนใหญ่ใช้การเข้ารหัสแบบอสมมาตรประเภทเดียวกันเช่น RSA หรือที่เรียกว่า Elliptic Curve Cryptography แม้ว่าจะแตกต่างกัน แต่ทั้งคู่มีพื้นฐานมาจากแนวคิดที่คล้ายคลึงกันและการเข้าใจ RSA เป็นสิ่งสำคัญในการเพิ่มความเข้าใจในการเข้ารหัสที่ใช้ในเครือข่าย cryptocurrency.
พื้นหลังการเข้ารหัสและการเข้ารหัสแบบสมมาตรเทียบกับอสมมาตร
จนถึงปี 1970 การเข้ารหัสมีพื้นฐานมาจากการใช้คีย์สมมาตรเป็นหลัก ในอัลกอริทึมของคีย์สมมาตรผู้ใช้สองคนที่ต้องการสื่อสารข้อความถึงกันจะใช้คีย์การเข้ารหัสเดียวกันสำหรับทั้งการเข้ารหัสข้อความธรรมดาและการถอดรหัสของไซเฟอร์เท็กซ์ กุญแจแสดงถึงความลับร่วมกันระหว่างทั้งสองฝ่ายและสามารถใช้เป็นการสื่อสารแบบส่วนตัวได้ อย่างไรก็ตามมีปัญหาโดยธรรมชาติบางอย่างกับการออกแบบนี้ซึ่งนำไปสู่ข้อเสียที่ร้ายแรงบางประการในการใช้งาน.
ตัวอย่างเช่นทั้งสองฝ่ายจำเป็นต้องทราบคีย์ลับเพื่อเข้ารหัสและถอดรหัสข้อความ นอกเหนือจากการพบปะกันเพื่อแลกเปลี่ยนข้อมูลนี้แล้วยังมีค่าใช้จ่ายในการสื่อสารจำนวนมากที่จำเป็นในการดำเนินการนี้เป็นการส่วนตัวผ่านสื่อที่ไม่ปลอดภัย บุคคลที่สามที่รับชมช่องเหล่านี้อาจสามารถรับคีย์ลับได้ดังนั้นวิธีการเข้ารหัสจึงถูกบุกรุก นอกจากนี้แนวคิดของการเข้ารหัสคีย์สมมาตรไม่สามารถปรับขนาดได้ หากคุณต้องการส่งข้อความที่เข้ารหัสไปยังบุคคลหลายคนคุณจะต้องจดจำคีย์ลับสำหรับแต่ละสายการสื่อสารเหล่านั้น เห็นได้ชัดว่าสิ่งนี้ไม่สะดวกอย่างรวดเร็วและเห็นได้ชัดว่าไม่ใช่รูปแบบที่ดีที่สุดที่จะใช้กับเครือข่าย cryptocurrency ที่มีการแลกเปลี่ยนมูลค่า.
วิธีแก้ปัญหานี้มาในรูปแบบของสิ่งที่เรียกว่าการเข้ารหัสแบบอสมมาตรหรือที่นิยมเรียกกันว่า การเข้ารหัสคีย์สาธารณะ. การเข้ารหัสแบบไม่สมมาตรใช้สองคีย์คือคีย์สาธารณะและคีย์ส่วนตัว ในรูปแบบพื้นฐานที่สุดของโมเดลนี้ผู้ใช้สามารถเผยแพร่คีย์สาธารณะซึ่งทุกคนสามารถใช้เพื่อส่งข้อความเข้ารหัสถึงบุคคลนั้นได้และมีเพียงผู้ที่เผยแพร่คีย์สาธารณะและมีคีย์ส่วนตัวที่เกี่ยวข้องเท่านั้นที่สามารถถอดรหัสและดูข้อความนี้ได้ การใช้คีย์หนึ่งจะยกเลิกการใช้คีย์อื่น ๆ และคีย์ไม่จำเป็นต้องแลกเปลี่ยนระหว่างฝ่ายที่ต้องการสื่อสาร.
รูปแบบการเข้ารหัสแบบอสมมาตรเกิดขึ้นได้จากหลักการที่ยอดเยี่ยม 2 ประการซึ่งเป็นผลมาจากการพัฒนาโดย James Ellis นักคณิตศาสตร์ชาวอังกฤษในปี 1970 เอลลิสอธิบายถึงแนวคิดที่การเข้ารหัสและการถอดรหัสเป็นการดำเนินการผกผันซึ่งกันและกันโดยอาศัยคีย์ที่ต่างกัน 2 คีย์.

James Ellis ภาพจาก โทรเลข.
โดยทั่วไปแนวคิดนี้จะแสดงด้วยแม่กุญแจและกุญแจโดยแม่กุญแจจะแสดงถึงคีย์สาธารณะและคีย์ที่แสดงถึงคีย์ส่วนตัว ในการใช้ทฤษฎีนี้ในทางปฏิบัติหลักการสองประการได้พัฒนาขึ้น.
ฟังก์ชัน Trapdoor
ฟังก์ชันประตูลับเป็นแนวคิดที่สำคัญมากในการเข้ารหัสซึ่งเป็นเรื่องเล็กน้อยที่จะเปลี่ยนจากสถานะหนึ่งไปยังอีกสถานะหนึ่ง แต่การคำนวณในทิศทางตรงกันข้ามโดยการย้อนกลับไปยังสถานะเดิมนั้นเป็นไปไม่ได้หากไม่มีข้อมูลพิเศษหรือที่เรียกว่า “ประตูดัก”.
ฟังก์ชันทางดักที่รู้จักกันดีในปัจจุบันซึ่งเป็นพื้นฐานสำหรับการเข้ารหัส RSA เรียกว่า ตัวประกอบที่สำคัญ. โดยพื้นฐานแล้วการแยกตัวประกอบเฉพาะ (หรือที่เรียกว่า Integer Factorization) เป็นแนวคิดในทฤษฎีจำนวนที่ว่าจำนวนเต็มคอมโพสิตสามารถย่อยสลายเป็นจำนวนเต็มขนาดเล็กได้ จำนวนผสมทั้งหมด (จำนวนที่ไม่ใช่จำนวนเฉพาะ) ที่แยกย่อยออกเป็นพื้นฐานที่สุดประกอบด้วยจำนวนเฉพาะ กระบวนการนี้เรียกว่าการแยกตัวประกอบเฉพาะและมีผลกระทบร้ายแรงเมื่อนำไปใช้กับการเข้ารหัส.
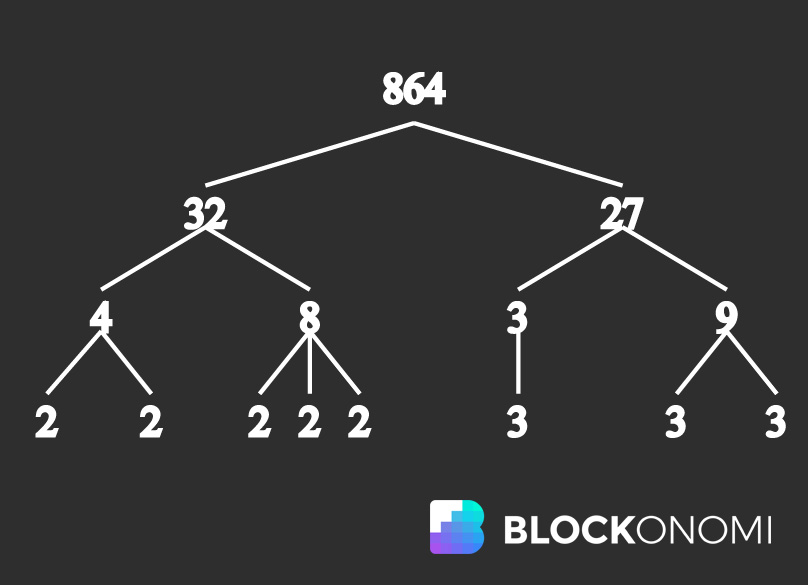
Prime Factorization ภาพที่ใช้จาก Wikipedia
โดยพื้นฐานแล้วการแยกตัวประกอบเฉพาะของจำนวนเฉพาะที่มีขนาดใหญ่มากนั้นไม่สามารถคำนวณได้เนื่องจากจำนวนการทดลองและข้อผิดพลาดที่จำเป็นในการแยกตัวประกอบจำนวนเข้ากับส่วนประกอบพื้นฐานที่สุดได้สำเร็จ ปัจจุบันไม่มีอัลกอริทึมการแยกตัวประกอบที่มีประสิทธิภาพเพื่อดำเนินการนี้.
RSA และวิธีใช้การแยกตัวประกอบเฉพาะมีอธิบายไว้ในส่วนต่อไป แต่ก่อนอื่นเราต้องเข้าใจการแลกเปลี่ยนคีย์ Diffie-Hellman.
การแลกเปลี่ยนคีย์ Diffie-Hellman
การแลกเปลี่ยนคีย์ Diffie-Hellman เป็นหนึ่งในโปรโตคอลการเข้ารหัสคีย์สาธารณะแบบแรกและโดยพื้นฐานแล้วอนุญาตให้แลกเปลี่ยนคีย์การเข้ารหัสผ่านสื่อสาธารณะได้อย่างปลอดภัย เพื่อความเรียบง่ายการพยายามสร้างแนวคิดของการแลกเปลี่ยนคีย์ Diffie-Hellman และส่วนต่อไปนี้เกี่ยวกับวิธีการทำงานของอัลกอริทึม RSA มีความซับซ้อนมากกว่าแนวคิดนามธรรมเมื่อเทียบกับคณิตศาสตร์บริสุทธิ์ดังนั้นเราจะใช้คณิตศาสตร์เมื่อจำเป็นเท่านั้น.
ตัวอย่างที่พบบ่อยที่สุดที่ใช้ในการกำหนดแนวคิดการแลกเปลี่ยนคีย์ Diffie-Hellman เรียกว่าการแลกเปลี่ยนสีลับ.
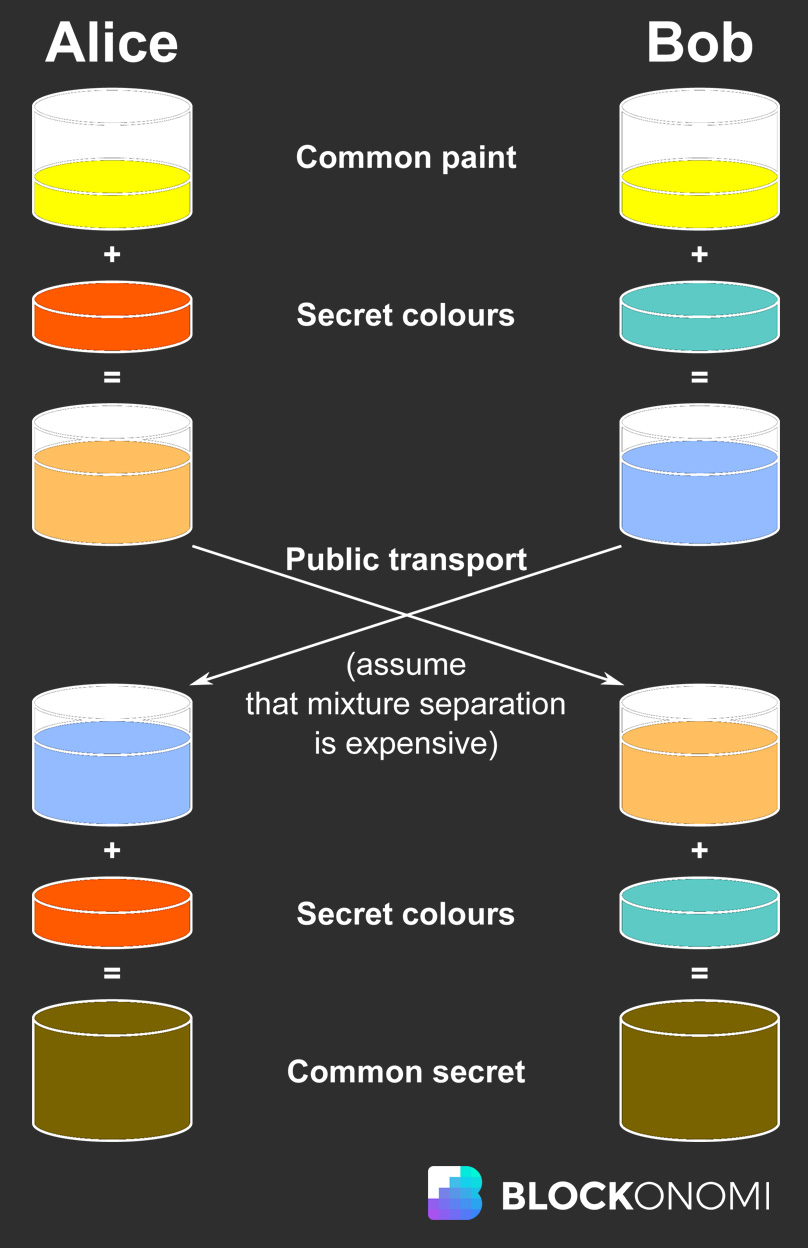
Diffie-Helman Key Exchange รูปภาพที่ใช้จากไฟล์ Wikipedia
รูปภาพด้านบนแสดงถึงแนวการสื่อสารระหว่างอลิซและบ็อบผ่านช่องสาธารณะที่อีฟสามารถรับฟังทุกสิ่งที่สื่อสารแบบสาธารณะระหว่างอลิซและบ็อบ ดังนั้นอลิซและบ็อบจะสื่อสารข้อความส่วนตัวโดยใช้การเข้ารหัสแบบอสมมาตรได้อย่างไรโดยไม่ต้องแลกเปลี่ยนข้อมูลนั้นอย่างชัดเจนผ่านสื่อสาธารณะ?
พวกเขาแลกเปลี่ยนข้อมูลลับซึ่งกันและกันโดยไม่เปิดเผยจริงๆ กระบวนการทำงานดังนี้:
ขั้นตอนที่ 1
- อลิซและบ็อบยอมรับว่าสีเหลืองเป็นสีที่ใช้กันทั่วไป ข้อมูลนี้ออกอากาศผ่านช่องสาธารณะเพื่อให้อีฟรู้เรื่องนี้เช่นกัน.
- สีเหลืองหมายถึงกุญแจสาธารณะ.
- อลิซตัดสินใจอย่างลับๆว่าเธอจะใช้ Blue ร่วมกับ Yellow และ Bob ก็แอบตัดสินใจว่าจะใช้ Red กับ Yellow.
- สีน้ำเงินที่ Alice และ Red ใช้โดย Bob แทนกุญแจลับของพวกเขา.
ขั้นตอนที่ 2
- จากนั้นทั้งอลิซและบ็อบจะผสมสีลับกับสีเหลืองเพื่อสร้างสีผสม.
- ส่วนผสมของ Alice สร้างส่วนผสมของ Green และ Bob ทำให้เกิด Orange.
- ตอนนี้ทั้งอลิซและบ็อบต่างส่งสีผสมซึ่งกันและกัน.
- อีฟได้รับสีเหล่านี้เช่นกัน แต่ประสบปัญหาสีผสมเหล่านี้แสดงถึงฟังก์ชันประตูกั้น.
- เป็นเรื่องง่ายที่จะรวมสองสีเพื่อสร้างสีที่สาม แต่กลับไม่สามารถทำได้ เป็นเรื่องยากมากที่จะระบุว่าสีใดถูกใช้เพื่อสร้างสีที่สามจากการมีเพียงสีที่สามและสีเหลืองดั้งเดิม.
ขั้นตอนที่ 3
- จากนั้นอลิซและบ็อบผสมสีลับกับสีผสมที่ได้รับซึ่งส่งผลดังต่อไปนี้.
- Alice ผสม Blue กับ Orange จาก Bob.
- Bob ผสม Red กับ Composite Green จาก Alice.
- สารผสมทั้งสองส่งผลให้เป็นสีน้ำตาล.
นั่นคือความลับของการแลกเปลี่ยนคีย์ Diffie-Hellman แม้ว่าทั้งอลิซและบ็อบจะลงเอยกับบราวน์ แต่พวกเขาก็ไม่เคยแลกเปลี่ยนสีนั้นจริง ๆ และอีฟก็ถูกทิ้งไว้โดยไม่มีข้อมูลที่จำเป็นของสีลับเพื่อให้สามารถคำนวณข้อความลับได้ (สีน้ำตาล).
ตัวอย่างข้างต้นเป็นภาพที่เรียบง่ายมากว่าการแลกเปลี่ยนทำงานอย่างไร ด้วยการประยุกต์ใช้คณิตศาสตร์การรักษาความปลอดภัยที่มั่นใจได้และความสมบูรณ์ของข้อความสามารถทำได้ผ่านการเข้ารหัส RSA โดยใช้การแยกตัวประกอบเฉพาะเป็นประตูประตู.
อัลกอริทึม RSA ทำงานอย่างไร?
อัลกอริทึม RSA ทำงานโดยใช้ช่องดักตัวประกอบเฉพาะและการแลกเปลี่ยนคีย์ Diffie-Hellman เพื่อให้เกิดการเข้ารหัสแบบไม่สมมาตร โดยพื้นฐานแล้วการเข้ารหัส RSA อาศัยความยากลำบากในการแยกตัวประกอบเฉพาะเป็นวิธีการรักษาความปลอดภัย อัลกอริทึม RSA มี 4 ขั้นตอนด้วยตัวอย่างที่เรียบง่ายมากพร้อมการอธิบายคณิตศาสตร์แบบ จำกัด.
- การสร้างคีย์ – ในขั้นตอนนี้ผู้ใช้สามารถใช้ตัวสร้างตัวเลขสุ่มหรือเลือกจำนวนเฉพาะที่มีขนาดใหญ่มาก 2 ตัว (เรียกว่า p และ q) ตัวเลขเหล่านี้จะต้องถูกเก็บเป็นความลับ คำนวณ n = pq โดยที่“ n” เป็นโมดูลัสของทั้งคีย์สาธารณะและคีย์ส่วนตัวและความยาวของคีย์นั้นเรียกว่าความยาวของคีย์ กำหนดให้“ n” เป็นสาธารณะ สำหรับคีย์ที่มีขนาดเท่ากับหรือมากกว่า 1024 บิตไม่มีวิธีที่มีประสิทธิภาพในการแก้อัลกอริทึมนี้ แม้แต่ซูเปอร์คอมพิวเตอร์ที่ใหญ่ที่สุดในโลกก็ยังต้องใช้เวลาหลายพันปีในการแก้ไขปัญหานี้ สิ่งนี้เรียกว่าปัญหา RSA และหากแก้ไขได้จะทำให้ระบบเข้ารหัสที่ใช้ RSA ทั้งหมดเสียหาย.
- การกระจายคีย์ – Bob ต้องการส่งข้อมูลลับของ Alice เพื่อให้ขั้นตอนต่อไปนี้เกิดขึ้น.
- บ็อบต้องรู้คีย์สาธารณะของอลิซเพื่อเข้ารหัสข้อความ.
- อลิซต้องรู้คีย์ส่วนตัวของเธอเพื่อถอดรหัสข้อความ.
- เพื่อให้บ็อบสามารถส่งข้อความเข้ารหัสของเขาได้อลิซจึงส่งคีย์สาธารณะของเธอให้บ็อบ.
- อลิซไม่เคยแจกจ่ายคีย์ส่วนตัวของเธอ.
สามารถดูคำอธิบายเชิงลึกเพิ่มเติมเกี่ยวกับการดำเนินการทางคณิตศาสตร์ที่ใช้ใน RSA ได้ ที่นี่, แต่อยู่นอกขอบเขตของบทความนี้.
นอกจากนี้การเข้ารหัส RSA ยังช่วยให้สามารถเซ็นข้อความแบบดิจิทัลซึ่งเป็นสิ่งสำคัญยิ่งสำหรับสกุลเงินดิจิทัลและเป็นองค์ประกอบสำคัญของรูปแบบธุรกรรม UTXO ของ Bitcoin อลิซสามารถเซ็นข้อความแบบดิจิทัลถึงบ็อบเพื่อยืนยันว่าเธอส่งไป (โดยการตรวจสอบว่ามีการใช้คีย์ส่วนตัวของเธอ) ผ่านการสร้างค่าแฮชของข้อความและแนบไปกับข้อความ ค่านี้สามารถตรวจสอบได้โดย Bob ซึ่งใช้อัลกอริทึมแฮชเดียวกันร่วมกับคีย์สาธารณะของ Alice และเปรียบเทียบค่าแฮชที่ได้กับค่าแฮชจริงของข้อความ.
สรุป
การเข้ารหัส RSA เป็นวิธีการเข้ารหัสแบบอสมมาตรที่ใช้กันอย่างแพร่หลายมากที่สุดในโลกเนื่องจากความสามารถในการเข้ารหัสระดับสูงโดยไม่มีอัลกอริทึมที่เป็นที่รู้จัก แต่ยังไม่สามารถแก้ไขได้ จากความก้าวหน้าที่ยอดเยี่ยมในการเข้ารหัสและคณิตศาสตร์รวมถึงการแลกเปลี่ยนคีย์ Diffie-Hellman และฟังก์ชันประตูลับการเข้ารหัส RSA กลายเป็นสิ่งสำคัญยิ่งในการรักษาความปลอดภัยการสื่อสารทั่วโลก.



