رمزنگاری منحنی بیضوی چیست؟ فناوری پشت امضاهای دیجیتال در ارزهای رمزپایه

رمزنگاری زیربنای طرح های امضای دیجیتال ارزهای رمزپایه است و پایه ای برای تأیید معامله امن آنها بین دو طرف در یک شبکه غیرمتمرکز است. امروزه روش های رمزنگاری متعددی وجود دارد که توسط ارزهای رمزپایه مختلف مورد استفاده قرار می گیرد و تمرکز آنها بر ارائه مدل های معاملاتی کارآمد و ایمن است.

رمزنگاری منحنی بیضوی (ECC) یکی از روشهای پرکاربرد برای طرحهای امضای دیجیتال در ارزهای رمزنگاری شده است و یک طرح خاص ، الگوریتم امضای دیجیتال منحنی بیضوی (ECDSA) در هر دو بیت کوین و اتریوم برای امضای معاملات اعمال می شود.

پیش زمینه ECC و ECDSA

رمزنگاری منحنی بیضوی توسط ریاضیدانان نیل کوبلیتز و ویکتور اس میلر ، به طور مستقل ، در سال 1985 پیشنهاد شد. در حالی که دستیابی به موفقیت در رمزنگاری ، از ECC تا اوایل سال 2000 ، در هنگام ظهور اینترنت ، جایی که دولت ها و ارائه دهندگان اینترنت شروع به استفاده از آن کردند ، به طور گسترده ای مورد استفاده قرار نگرفت به عنوان یک روش رمزگذاری.

در مقایسه با رمزگذاری RSA ، ECC یک مزیت قابل توجه را ارائه می دهد. اندازه کلید مورد استفاده برای ECC بسیار کمتر از آنچه برای رمزگذاری RSA لازم است است ، در حالی که هنوز همان سطح امنیتی را فراهم می کند. اگرچه امروزه رمزگذاری RSA در اینترنت بیشتر مورد استفاده قرار می گیرد ، اما ECC اساساً شکل کارآمدتری از RSA است که یکی از دلایل اصلی استفاده از آن در ارزهای رمزپایه است..

بخوانید: رمزنگاری RSA چیست؟ راهنمای کامل این الگوریتم رمزگذاری

انستیتوی استاندارد و فناوری ملی ایالات متحده (NIST) ECC را به عنوان “مجموعه Bالگوریتم های توصیه شده ، و NSA رسماً از طبقه بندی اطلاعات بسیار محرمانه با کلیدهای 384 بیتی پشتیبانی می کند. به عنوان مثالی از کارایی ECC در مقایسه با RSA ، همان کلید 384 بیتی مورد استفاده در رمزگذاری اطلاعات طبقه بندی شده به یک کلید 7680 بیتی با استفاده از رمزگذاری RSA نیاز دارد. بنابراین کارایی ارائه شده توسط ECC برای شبکه های بلاکچین بسیار مفید است ، زیرا حجم معاملات را کاهش می دهد.

چگونه کار می کند

رمزنگاری منحنی بیضوی روشی است برای کلید عمومی رمزگذاری بر اساس عملکرد جبری و ساختار منحنی بیش از یک نمودار محدود. از یک تابع trapdoor استفاده می کند که بر عدم امکان تعیین لگاریتم گسسته یک عنصر منحنی بیضوی تصادفی دارای یک نقطه پایه شناخته شده عمومی است.

توابع Trapdoor در رمزنگاری با کلید عمومی استفاده می شود تا از A -> B بی اهمیت است ، اما رفتن از B -> A با استفاده از یک مسئله خاص ریاضی غیرقابل اجرا است. به عنوان مثال ، رمزگذاری RSA براساس مفهوم فاکتور سازی نخست, و ECC به مفهوم ضرب نقطه ای, که در آن ضرب نمایانگر کلید خصوصی است و محاسبه از مبادی شروع غیرممکن است.

منحنی بیضوی باید از نقاطی تشکیل شود که معادله را برآورده می کند:

y ^ 2 = تبر ^ 3 + ب

(x، y) روی منحنی یک نقطه را نشان می دهد ، در حالی که هر دو a و b ثابت هستند. از لحاظ تئوری ، منحنی های نامحدودی وجود دارد که می تواند ایجاد شود ، اما به طور خاص در ارزهای رمزپایه اعمال می شود (در مورد بیت کوین و اتریوم) ، منحنی بیضوی خاصی به نام secp256k1 استفاده می شود. در تصویر زیر نشان داده شده است.

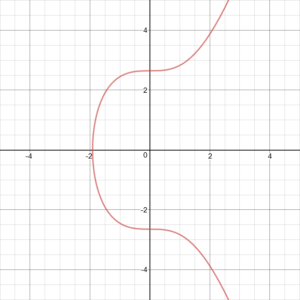
همانطور که می بینید ، منحنی های بیضوی در مورد محور x متقارن هستند. به همین دلیل ، اگر از یک نقطه تصادفی روی منحنی یک خط مستقیم بکشید ، خط منحنی را در بیش از 3 نقطه قطع نمی کند. شما از طریق دو نقطه اول یک خط می کشید و محل تلاقی خط با نقطه سوم را تعیین می کنید. بعد ، آن نقطه سوم را در محور x منعکس می کنید (متقارن است) و آن نقطه نتیجه جمع شدن دو نقطه اول با هم است. این در تصویر زیر نشان داده شده است.

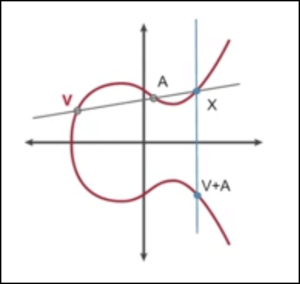
در نمودار بالا ، V و A نشان دهنده نقاط شروع است ، X نشان دهنده نقطه سوم است و نقطه آخر (بگذارید آن را Z بنامیم) نشان دهنده جمع كردن V و A با هم است. هنگامی که در طرح امضای دیجیتال استفاده می شود ، نقطه پایه خط به طور معمول از پیش تعریف شده است.

برای ایجاد تابع trapdoor توسط ECC ، رمزنگاری منحنی بیضوی از ضرب نقطه استفاده می کند ، جایی که نقطه پایه شناخته شده به طور مکرر به خودش اضافه می شود. در چنین حالتی ، بیایید از یک نقطه پایه P استفاده کنیم ، جایی که هدف یافتن 2P است ، همانطور که در زیر توضیح داده شده است.

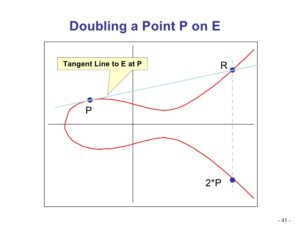
در بالا ، یک مماس از نقطه P تا نقطه R عبور می کند که نقطه تلاقی است. بازتاب آن نقطه 2P است. فرض کنید می خواهیم این کار را ادامه دهیم و 3P ، 4P و غیره را پیدا کنیم. بعد ، ما به P و 2P می پیوندیم و متعاقباً این نقطه را در تقاطع منعکس می کنیم ، و این کار را برای 4P ادامه می دهیم. در زیر نشان داده شده است:

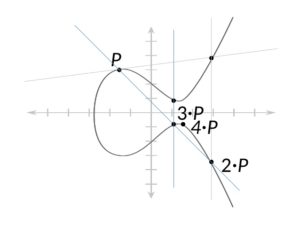
این خاصیت ضرب نمودار است زیرا ما در حال یافتن نقاطی هستیم که ضرب یک عدد صحیح با خود نقطه هستند. نتیجه همان چیزی است که عملکرد را trapdoor خود می دهد ، معروف به مشکل لگاریتم گسسته.

اگر یک متغیر x را به عنوان یک عدد صحیح 384 بیتی نشان دهیم و آن را با نقطه پایه P ضرب کنیم ، نتیجه یک نقطه روی منحنی است که Z نامیده می شود. برای ارزهای رمزپایه اعمال می شود ، Z عمومی است ، اما متغیر اصلی x مخفی است (خصوصی کلید) برای تعیین x از Z و P ، باید چند بار P به خود اضافه شود تا نقطه Z روی منحنی بدست آید. این مشکل نوعی از است حساب ماژولار این از نظر ریاضی غیرقابل اجرا است و به همین دلیل ECC بسیار امن است.

در ارزهای رمزپایه استفاده کنید

هنگام تجزیه و تحلیل نیاز به طرح های امضای دیجیتال در ارزهای رمزپایه ، 4 مورد اصلی هر طرح داده شده وجود دارد که باید برای اثبات قابل اعتماد بودن و قابل تأیید بودن طرح امضا برآورده شود. این شامل:

باید اثبات شود که امضا کننده یک معامله امضا کننده است.
امضا نباید جعلی باشد.
امضا لازم نیست قابل سرزنش باشد ، به این معنی که امضاها نهایی هستند و نمی توانند با هویت دیگری همراه باشند.
استخراج کلید خصوصی از یک کلید عمومی مربوطه از نظر محاسباتی غیرممکن است.

رمزنگاری منحنی بیضوی هر 4 شرایط را برآورده می کند و همچنین به ویژه در انجام آن موثر است. با استفاده از ECC ، مختصات (x ، y) یک نقطه روی نمودار ، کلید عمومی شما و عدد صحیح تصادفی 384 بیتی x ، کلید خصوصی شما خواهد بود..

همچنین می توان به کسی ثابت کرد که شما مقدار x را می دانید ، بدون اینکه مشخص کنید x چیست. این ویژگی بیشتر به تأمین شرایط لازم برای استفاده پایدار در طرح معاملات امضای دیجیتال کمک می کند.

نگرانی های کوانتومی

استفاده از ECC در طرح های امضای دیجیتال برای ارزهای رمزپایه بسیار امن است. با این حال ، اخیراً نگرانی هایی در مورد پتانسیل آینده رایانه های کوانتومی و قدرت قابل توجه آنها در توانایی شکستن ECC مطرح شده است. گرچه احتمال آن سالها فاصله دارد, الگوریتم Shor از نظر تئوری قادر به محاسبه لگاریتم های گسسته بر روی یک رایانه کوانتومی فرضی با قدرت کافی است.

ارزهای رمزنگاری شده مختلف با اجرای الگوریتم های مقاوم در برابر کوانتوم به عنوان پایه و اساس طرح های امضای دیجیتالی خود ، رویکرد آینده نگرانه ای نسبت به تهدید احتمالی ایجاد شده توسط رایانه های کوانتومی در پیش گرفته اند. حتی NSA در سال 2015 انتقال آینده برنامه ریزی شده خود را به دور از ECC و به مجموعه رمزهای متفاوتی برای نیازهای رمزگذاری خود به دلیل اجتناب ناپذیری قدرت محاسبات کوانتومی اعلام کرد..

بخوانید: محاسبات کوانتومی: چه تهدیدی برای بیت کوین ایجاد می کند?

این نگرانی ها در درجه اول حدس و گمان در این مرحله است ، زیرا قدرت محاسبات کوانتومی لازم برای الگوریتم Shor برای محاسبه لگاریتم های گسسته قابل ملاحظه ای حتی از قدرتمندترین رایانه های کوانتومی مرحله اولیه موجود است.

نتیجه

با نگاه به آینده ، نسل های متوالی ارزهای رمزنگاری شده ممکن است در نهایت برای اطمینان از معاملات خود به روش های رمزگذاری پیشرفته تری روی بیاورند و به طور بالقوه ممکن است بیت کوین و اتریوم نیز نیاز به همان انتقال داشته باشند.

در حال حاضر ، ECC و سایر طرح های امضای دیجیتال با استفاده از توابع trapdoor برخی از امن ترین روش های رمزگذاری در جهان هستند و باید برای مدتی همچنان ادامه داشته باشند.